麦田怪圈真相解密-多维宇宙
麦田怪圈是人们的恶作剧还是来自其它世界的信息?它似乎在向我们讲述它来自另一个世界——多维宇宙!
I.圆平面的形成,

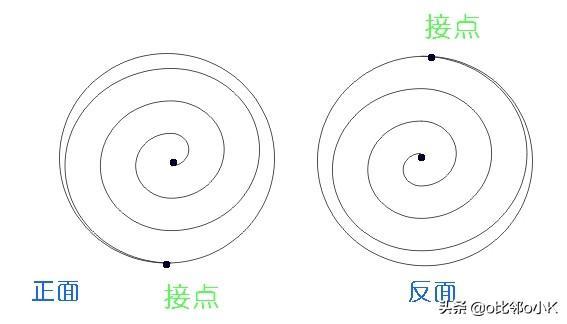
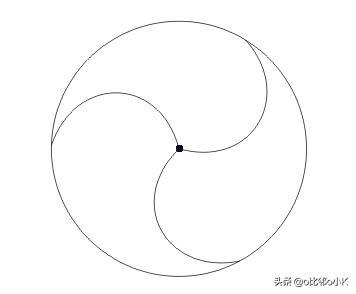
外面的大圆表示一个2D圆平面,我们把上半部分的螺旋中心点移到大圆的圆心
假设平面中从圆心发出的螺旋线足够长,足够密,那么它足以围成一个2D的圆平面;
同理,麦圈下半部分螺旋线是对另一面的描述。(平面的正反两面)
螺旋上与大圆圆心重合的点表示平面“正反两面”的“接点”,
“接点”位于圆平面的边界。
实例:(理解这一基本概念的可以跳过)
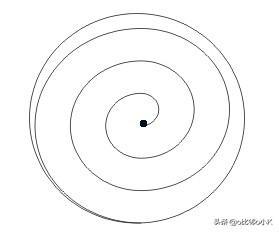
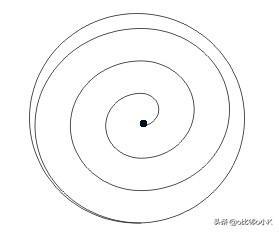
在一个圆形纸片的一个面上,笔尖从圆心开始向外逆时针绕圆心作螺旋运动,
只要笔尖运动轨迹足够密,旋转圈数足够多,
笔尖的运动轨迹将足以覆盖圆纸片的整一个面!
接着,笔尖在不离开这个圆纸片的情况下通过“接点”跨过边界,
到达纸片的另一面,然后向里以顺时针绕圆心作螺旋运动,最后回到圆心。
此时笔尖运动轨迹已完全覆盖了圆纸片的两面。
这里要说明的是任何维度的空间都有“接点”或“接线”“接面”……取决于维度的高低。
二维平面的接点只能在三维空间内才能看到,三维空间的“接线”只能在4维空间内看到。
通过以上分析得出以下结论:
点和“由以自身为中心,螺旋运动产生的轨迹(曲线)”的“无缝接合”形成平面--------(1 )表示为:
或者,螺旋线以一端为中心旋转产生的轨迹形成平面
表示为:
两种运动都是等效的。
II.三维球体的形成。
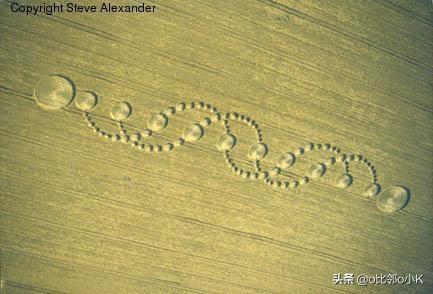
来看另一幅麦圈:

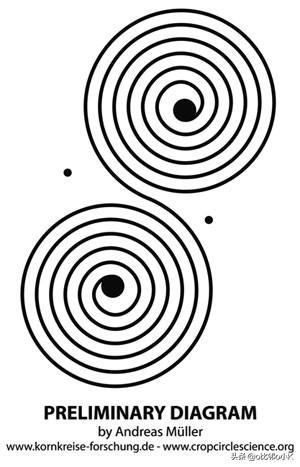

有点像苹果的表面展开图,其实就是球面的展开图! 这幅麦圈给我们一个明显的提示:
(我相信一些聪明的朋友已经看出来了,并且举一反三,能推理出3D球体的形成过程了!!)
形成球面的点的运动轨迹在2D平面上的投影与形成2D平面的点的运动轨迹相同!――――(2)
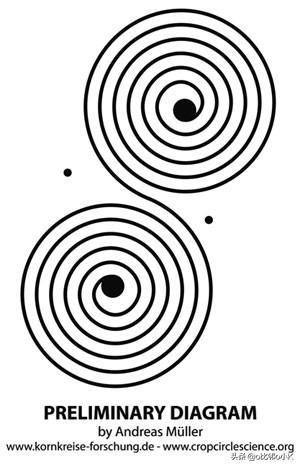
然后呢?? 有兴趣的可以自已尝试推理,这样有益于开发你意识的灵性!
现在我们把形成半球面的两点用一条线段连接,并保持线段的长度不变,以线段的中点为螺旋
中心运动。发现线段的扫过的轨迹(曲面)就像两个相连不断扩大的锥面,两锥面的无数次叠加
形成了球体,线段两端点的运动轨迹的叠加则为3D球体的一个层面,即球面。
通过以上分析,可得出以下结论:
线和“由以自身为中心,螺旋运动产生的轨迹(曲面)”的“无缝接合”形成三维球体―――(3)
我们知道“点”表0维,“线”表示1维,“面”表示2维,“体”表示3维
由(1),(3)我们可以推导出一条通式:
点和“由以自身为中心,螺旋运动产生的轨迹(曲线)”的“无缝接合”形成平面--------(1 )
0D+(2D中的)1D=2D
线和“由以自身为中心,螺旋运动产生的轨迹(曲面)”的“无缝接合”形成三维球体―――(3)
1D+(3D中的)2D=3D
所以nD+(n+1)D=(n+2)D (n为自然数) ――― (4)
n维空间和“由以自身为中心,螺旋运动产生的轨迹(n+1维)”的“无缝接合”形成(n+2)维空间
二维空间的表面由一维曲线层层叠加形成,一维曲线是二维空间的一个层线
三维空间的表面由二维曲面层层叠加形成,二维曲面是三维空间的一个层面。
同理:
四维空间的表面由三维曲体层层叠加形成,三维曲体是四维空间的一个层体。
(我们被困在了这个三维曲体中)
因此四维“球状物”表面的螺旋运动轨迹在三维空间的投影为球体上的螺旋运动轨迹,而球体表面是二维的曲面,所以球体上的螺旋运动轨迹在二维平面上的投影为螺旋线。因此四维空间的球状物表面的螺旋运轨迹在二维平面的投影仍为螺旋线。 ――― (5)
任何维度的螺旋运动轨迹都能在二维平面中,以点螺旋运动产生的轨迹表示。 ―――(6)
由(4)nD+(n+1)D=(n+2)D (n为自然数)当n=2时,便可以描述四维空间的形成过程
面和“由以自身为中心,螺旋运动产生的轨迹(曲体)”的“无缝接合”形成四维球状物



以上三幅麦圈是表示四维球状物形成过程的等效图。(详见 结论(5)和(6))
关于麦比乌斯圈:
上图表示纸条的一条边界与另一条边界相接形成一个麦比乌斯圈。

上图表示一条纸带在空间的形态,用网格标识这条纸带的一个面。
想像有一条围绕地球表面的纸条(曲面),纸条一端在南极,另一端在北极。
纸条的同一个面始终紧贴地球,所以紧贴北极的一面朝下,紧贴南极的一面朝上,
与麦圈所表达的意思等效。如果把两端对接(相当于左手掌心与右手掌心合拢,拇指与小指对齐)
形成的圈,就是麦比乌斯圈。如果纸带足够长,曲率合适,那么这条纸带则可以覆盖球面。
球面的叠加形成球体,因此二维麦比乌斯圈的叠加则形成三维球体,
同理,三维麦比乌斯圈的叠加形成四维球状物
N维麦比乌斯圈叠加形成N+1维空间两个2D麦比乌斯圈叠加:

N维麦比乌斯圈叠加(旋转表示无限叠加),表示多维宇宙: