几何学的诞生过程——欧几里得和他的毕氏定理

第2章 自然秩序中的几何
因为你瞧,这整出宇宙大戏——
粒子、原子、星辰和其他物质的复杂舞蹈,
不断地游移、运动与相互作用——
都是在同一个舞台上演出,
或可说,在一个“空间”之内上演。
如果不能掌握空间的详细特征,
便不能真正理解这出戏。
在欧洲或西方传统过去2500年的大部分时间里,研究几何是因为,几何被认为是除了天启之外,人类所能拥有的最为精致、完美、堪为典范的真理。在某种方式上,几何彰显了物理世界最深刻的真实本质。
——波希—霍尔(Piers Bursill-Hall),
《我们为何要学几何?》
几何是什么?许多人认为它不过是高中时的一门课,一套测量直线之间的夹角,计算三角形、圆形、矩形面积的技巧,或者是建立不同物体之间是否相似或全等的度量方式。但即使采用这么有限的定义,几何也无疑是一项有用的工具:比方说,建筑师就天天用得着。这些当然是几何的范畴,但几何远不止于此,因为确实在建筑的最广义层次上,从至微到至巨的尺度,全都离不开几何。而对于像我这样,着迷于理解空间的尺寸、形状、曲率和结构的人而言,几何更是一项重要的工具。
“Geometry”(几何)这个字源自于“geo”(地)和“metry”(测量),原意是指“测量土地”。不过我们现在更广义地用它来指测量空间,而空间本身则又不是一个明确定义的概念。诚如黎曼所云,“几何预设了空间的概念,并假定了空间构造的基本原理”,然而同时也赋予“这些事物仅仅名义上的定义”。[31]
虽然听来奇怪,但是让空间概念保持模糊是很有用的,因为它可以把很多我们难以命名的概念蕴含在内,所以暧昧反而能够带来某些便利。例如,当我们思索空间有多少维度,或是考虑空间的整体形状时,或许我们所指的也是整个宇宙。空间可以狭义地定义成只是指一个简单的几何构造,如点、线、面或甜甜圈之类中小学生常会画的图形;或者,空间也可以更抽象、更复杂,而且远远更难描绘。
比方说,假如你有一堆点,以某种复杂、混乱的配置方式散布开来,而且毫无办法判定各点之间的距离,对数学家而言,这个空间就没有几何结构,它们只是一群随机组成的点。然而,一旦加入称为“度规”(metric)的测量函数,以计算任意两点间的距离,那么你就突然有了一个可以在其间游移的空间,拥有明确定义的几何构造。换句话说,一旦空间有了度规,就具备让该空间成形的所有信息。一旦掌握这种测量能力,就可以非常精确地决定空间是否平坦,或者计算它偏离完全平坦的程度(称为曲率),这是我觉得最有趣的东西。
除非你认定几何不过是一把调校精准的直尺(这么说并非看轻直尺,我可是非常欣赏这项科技的),否则的话,几何是我们探索宇宙的主要大道之一。物理学和宇宙学,就它们的研究课题而言,对于理解宇宙是绝对必要的。几何在此的角色乍看之下并不那么明显,但却是同等重要的。我甚至认为,几何不仅能和物理学与宇宙学在同一基础上平起平坐,从许多方面来看,它就是基础。
因为你瞧,这整出宇宙大戏——粒子、原子、星辰和其他物质的复杂舞蹈,不断地游移、运动与相互作用——都是在同一个舞台上演出,或可说,在一个“空间”之内上演。如果不能掌握空间的详细特征,便不能真正理解这出戏。空间不仅仅是被动的背景,它其实赋予了宇宙最重要的内禀属性。事实上,就我们现在的理解,在空间中静止或移动的物质或粒子,其实就是空间(更精确地说是时空)的一部分。几何可以对时空、对物理系统整体给出限制,而这些限制是单纯从数学和逻辑的原理就可以推导出来的。
以地球的气候为例。虽然乍看之下并不明显,但气候是受到几何的深刻影响的,在此,最重要的因素是地球的形状是球形的,假如我们是住在二维的环面上,生命以及气候就会大为不同。正如第1章所提到过的,在球面上,风不能都往同一方向吹(例如都往东吹),海水不能都往同一方向流。必定会有某些地方,例如南、北极,风向或者洋流不是朝向东。“东”的观念在南、北极彻底消失了,所有运动在此都停止下来。但是单洞环面的情形就不一样了,上面并没有类似的停滞点,气流和海水全都可以毫无阻碍地朝向同一方面流动。(这种差别无疑会影响全球的循环模式,但若你想知道气候变化的种种细节,而且对球面和环面上的生活进行季节性比较,你还是得请教大气科学家。)
几何的应用范围还不仅止于此。例如,在爱因斯坦广义相对论的架构中,几何学已证明宇宙的物质和能量是正值,因此我们存身的四维时空是稳定的。几何原理也告诉我们,宇宙中必定存在一些称为“奇点”(singularity)的地方,例如黑洞的中心,在此物质密度会趋于无穷大,已知的物理性质不再适用。再以弦论为例,许多重要物理现象会发生在称为卡拉比—丘流形的奇特六维空间,卡拉比—丘流形的几何性质可以解释为何宇宙会有现在这许多基本粒子,不只决定它们的质量,也决定了它们之间的作用力。不仅如此,对这类高维空间的研究或许还能说明引力为何远比其他作用力微弱,同时也为宇宙诞生之初的暴胀机制,或现在推动宇宙扩张的暗能量等问题提供解答线索。
所以,当我说几何可与物理学和宇宙学等量齐观,都是解开宇宙奥秘的无价工具时,我并不是空口吹嘘。而且,随着下文将会提到的数学进展,再加上观测宇宙学的进步和弦论的到来(后者试图达成物理理论从未完成的大融合),这三个领域似乎同时汇聚在一起。结果人类知识如今正热切地向前推进,正要跨越重大突破的门槛,而在许多探索方向上,几何都担任了开路先锋的角色。
古希腊时代:毕氏定理与欧几里得
我们务必记住,不论我们在几何学上做出了什么,或是推动它朝哪个方向发展,这一切都不是全新开始的。我们总是援引前人的成果,不论它是猜想(即尚未得到证明的假设)、证明、定理或公设,都往往建立在数千年前奠立的基础上。在这个意义上,几何和其他科学一样,就像是精密的建筑工程。首先要打地基,如果施工正确,比方说,建造在坚固的岩石上,基础和地上建筑物就能稳固持久(只要它们也遵守坚实的规范施工的话)。而这基本上就是几何——我所选择的志向——的美感与力量之所在。当谈到数学时,我们总是预期“完全为真”的叙述,预期数学定理能成为永恒真理的精确叙述,其正确性不受空间、时间、群众观感和权威的影响。此一性质将它与其他经验式的科学区隔开来;在经验科学里,你得做实验,如果某项结果看起来不错,测试一段时间后没问题,你就接受其为真。但结论永远都有改变的可能,你永远无法期望一项发现是百分之百为真,永远不会改变的。
当然,我们经常会发现更广、更佳版本的数学定理,但这并不否定原来的定理。继续以建筑为比喻,如果建筑物的基础是稳固的,当我们进行增建和整修时,并不会去动到基础。有时我们所做的会超过整修的幅度,甚至或许会“打掉”隔间,重新规划内部格局。而即使旧定理仍然为真,我们会需要全新的发展,需要新的建材,以创造我们企图达到的全盘新貌。
最重要的定理通常会一次又一次被各种方式验证,基本上不可能有错。然而较冷门的定理,由于未受到如此仔细的验证,可能藏有问题。当发现错误时,建筑物的某个房间,甚至某个厢翼,或许需要拆掉重建。然而在此同时,这栋坚固的宅邸既已长期经受时间的考验,所以其他部分并不会受影响。
毕达哥拉斯是几何学领域的建筑大师,相传出自于他的那条公式是数学中建造得最坚固的宅邸之一,就是如今称为毕氏定理的式子,它说明直角三角形斜边长的平方等于两股的平方和。或者如同以前和现在的学生都记得的:a2+b2=c2。这是一条简单但威力强大的叙述,它在当代的重要性令人惊讶的程度仍不逊于约2500年以前的初创之时。毕氏定理的应用并不仅限于中学数学。其实,我差不多仍天天用到毕氏定理,由于浸淫已久,使用时完全不假思索。
在我看来,毕氏定理是几何学最重要的叙述。它不但在计算二维平面的习题作业或是中学课堂上的三维题目时是解题关键,且对于高深的高维数学,如计算卡拉比—丘空间中的距离,或是解爱因斯坦的运动方程式,也同等重要。毕氏定理的重要性源自于,我们可以用它算出在任何维度空间里,任意两点之间的距离。而且,正如我在本章一开始说的,几何和距离有密切的关系,这就是为什么毕氏定理几乎在一切几何问题里都是核心角色。
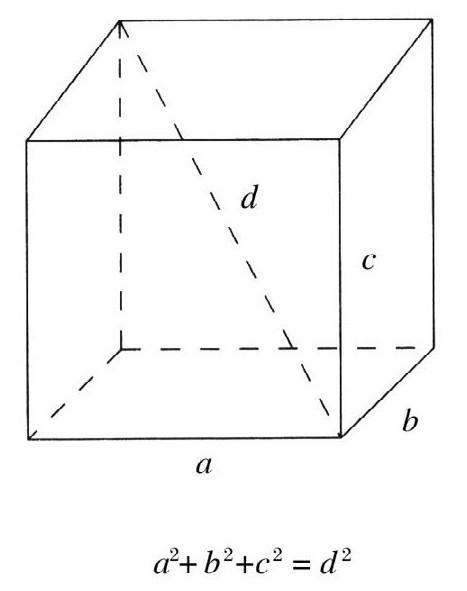
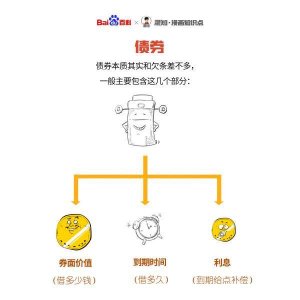
图2.1 毕氏定理通常用于描述二维平面上直角三角形的边长关系。但正如本图所示,毕氏定理同样可用于三维(a2+b2+c2=d2),甚至更高的维度
非但如此,我还觉得毕氏定理美丽绝伦——尽管我承认,美丽与否因人而异。我们倾向喜爱我们知道的东西,因为对它熟悉,感到自在,所以就像每天的日升日落一般被视为理所当然。再就是它言简意赅,只是三个字母的二次方,a2+b2=c2,简洁得犹如其他一些知名定律,如F=ma和E=mc2。对我而言,美感源于这条简单陈述如此怡然地身处在大自然之中所显现出来的优雅。
毕氏定理无疑是几何学的基石;但除了定理本身,同等重要的是它被“证明为真”的事实,而且应该是数学中第一个见诸记载的证明。早在毕达哥拉斯出生之前,埃及和巴比伦的数学家便已经使用直角三角形的三边关系,但是他们都不曾“证明”这个想法,而且似乎也不曾考虑过要去证明这种抽象概念。根据数学家贝尔(E.T.Bell)的说法,这才是毕达哥拉斯最伟大的贡献:
在他之前,几何大致只是一些经验法则的汇集,规则之间并没有清楚表明任何其中的相互关联。现在大家已理所当然把证明视为是数学的核心精神所在,我们很难想象在数学推理出现前必然会经历的原始状态。[32]
或许毕达哥拉斯确实给出过证明,但你也许已注意到,我说的是定理“相传”出自于他,仿佛对定理的著作权有所怀疑。确实如此。毕达哥拉斯是一个教派领袖般的人物,许多追随他的数学爱好者(称为毕氏学派)的贡献,后来都被归到他的名下。所以毕氏定理的证明也有可能是出自在他之后一两代的传人。真相我们大概永远不能确知:毕达哥拉斯活在公元前6世纪,几乎没有留下多少书面记录(甚至可说完全没有)。
幸运的是,欧几里得的情形很不一样。欧几里得是史上最知名的几何学家之一,几何之所以能成为一门精确、严格的学术领域,多半得归功于他。欧几里得迥异于毕达哥拉斯,身后留下了大量文献,其中最杰出的是约成书于公元前300年的《原本》。这是一部十三卷的著作,其中八卷专论平面和立体几何。《原本》被誉为有史以来最具影响力的教科书之一,“一部优美的著作,其影响力堪与圣经比拟。”物理学家兼编剧家曼罗迪诺(Leonard Mlodinow)在《欧几里得之窗》(Euclid’s Window)一书中如此形容。[33]
欧几里得在这部巨著里所奠立的,不只是几何学,而是一切数学的基础,它严格遵守了一种现今称为欧几里得式的推理方法:以明确定义的词汇和一组明白陈述的“公设”(英文是axiom或postulate,这两个词是同义的)为起点,然后运用清楚的逻辑来证明一条条定理,接着再用这些定理来证明其他命题。欧几里得以此方法,总共证明了四百多条定理,基本上囊括了当时所有的几何知识。
斯坦福大学数学家奥瑟曼(Robert Osserman)如此解释欧几里得方法的永恒魅力:“最重要的是确定感。在一个充满非理性信仰和无稽臆测的世界里,《原本》里的陈述一一被丝毫无疑地证明为真。”米莱(Edna St.Vincent Millay)在她的诗作(只有欧几里得见过赤裸之美)(Euclid Alone Has Looked on Beauty Bare)也表达了类似的欣赏。[34]
从微积分到微分几何
就本书所讨论的发展脉络而言,下一个重大贡献来自于笛卡儿(需要说明的是,在此略而未提的许多大数学家,并不表示他们的贡献并不重要)。正如第1章所述,笛卡儿导入了坐标系,使得数学家能够思考任何维度的空间,并且用代数来解决几何问题,从而大幅扩展了几何的视野。在他改写这个领域之前,几何学差不多就局限在直线、圆和圆锥曲线(conic sections)的讨论,圆锥曲线就是以不同角度切开一个无限长的圆锥时所得到的曲线,如椭圆、拋物线、双曲线。但一旦有了坐标系,一些本来不知道该如何描绘的复杂图形,便立刻可以借由方程式来描述。以xn+yn=1为例,使用笛卡儿坐标,我们可以解出这个方程式,然后再画出其曲线。在坐标系出现之前,我们不知如何画这样的图形。因此在以前遇到死路的地方,笛卡儿为我们指引了前进的方向。
大约在笛卡儿分享解析几何的概念五十年之后,牛顿(Isaac Newton)和莱布尼兹(Gottfried Leibniz)发明了微积分,把这条道路拓展得更宽广。其后数十年到数百年,欧拉(Leonhard Euler)、拉格朗日(Joseph Lagrange)、蒙日(Gaspard Monge)等数学家将微积分工具结合进几何里,而其中最重要的大概要属高斯(Carl Friedrich Gauss)的贡献了,经由他的指引,“微分几何”(differential geometry)这个领域终于在19世纪20年代成熟。微分几何把曲面摆到笛卡儿坐标系中,因而能使用微分的技巧加以详细分析(微分是找出平滑曲线斜率的技巧)。
微分几何的发展自高斯时代起即不断演进,诚然是一项重大成就。有了微积分工具之后,几何学家可以用较以往清晰的方式来刻画曲线和曲面的性质。几何学家通过微分来获取此类信息,其中微分就是求取导数(derivative),也就是测量函数如何随着输入值而变化的情形。
我们可以把函数想成是一种算则或公式,它收到一个输入的数,相应的就产生一个输出的值。以y=x2为例,给它x值,就可以产生y值,也就是x值的平方。函数具有一致的性质,如果你喂给它相同的输入值,就会得到相同的输出值。譬如在本例中,输入2,得到的必定是4。而导数则是用来描述当输入值变化时,输出值如何变化。导数值反映了当输入值发生微小改变时,输出值变化的敏感度。
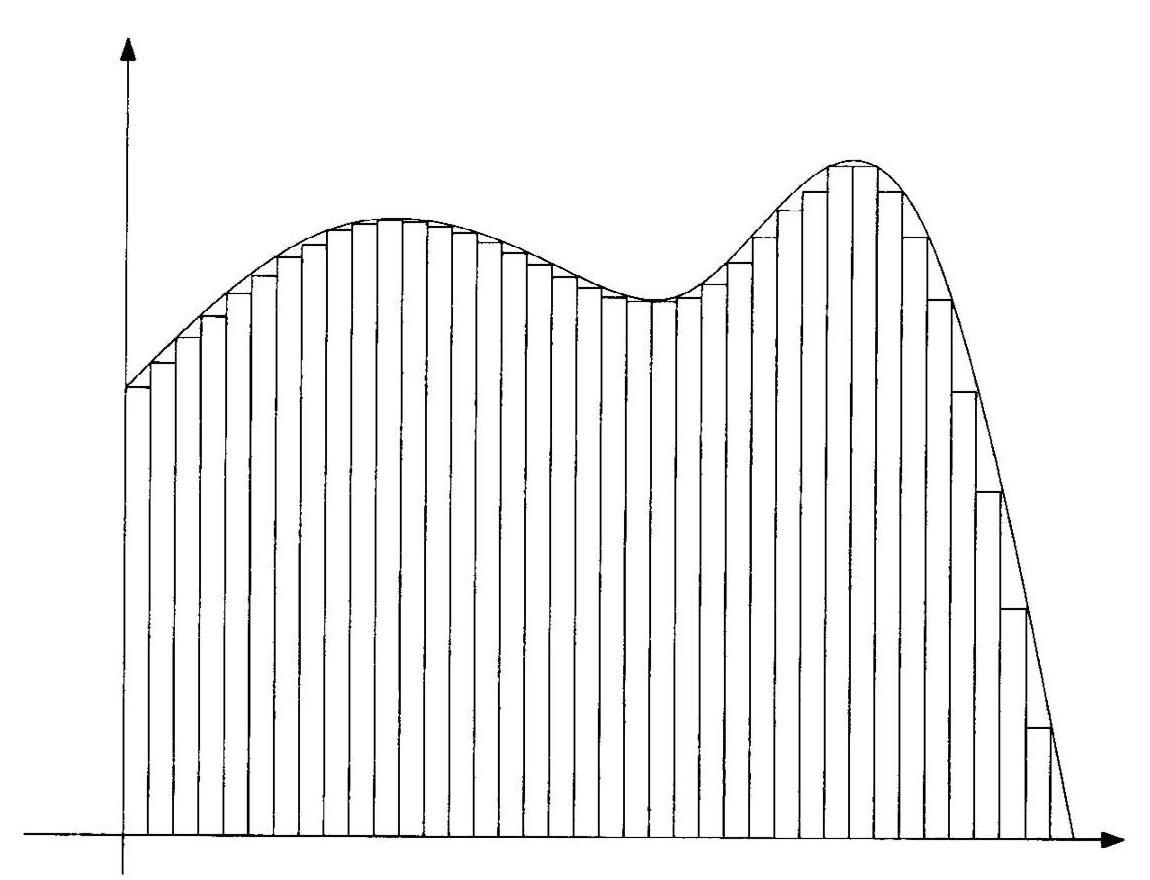
图2.2 我们可以用“积分”这个微积分的技巧来计算曲线围成的面积。把围成的区域分割成非常细小的矩形,再把所有矩形的面积相加起来,就可以得到面积的近似值。矩形的宽度愈窄,得到的近似值就愈准确:当分割到无穷小时,所得到的就是你要的值
导数并不只是某种抽象的概念,它是可经由计算得到的真实的数,能够明确告诉我们曲线或是曲面在某一点的斜率。比如说,在上述的例子里,我们可以明确决定该函数(这是一条拋物线)在x=2这一点的导数。如果我们从x=2移开一点点,例如移到x=2.001,y值会起什么变化?如果计算到小数点后三位的话,y值是4.004。而导数是输出值变化(0.004)对输入值变化(0.001)的比值,刚好是4。事实上这正是函数在x=2这一点的导数;或者换个说法,它是这条曲线(拋物线)在x=2这一点的斜率。
如果选择更复杂、更多维的函数,计算当然会变得更困难;不过我们暂时还是回到这个例子。我们计算y值变化对x值变化的比值来求得导数。这是因为导数就是函数在每一点的斜率或倾斜程度,而斜率正是测量y如何随着x的改变而变化。
换个方式来想,考虑曲面上的一点。如果把这一点往旁边移动一些,对它的高度有何影响?倘若这个曲面大致是平坦的,则高度变化不大。但若是这一点位于陡峭的斜坡上,高度的变化就会明显许多。导数所表示的就是一点所在位置附近的曲面斜率。
我们当然没必要局限在曲面上的一个点。借由对曲面上的各点求导数,我们可以精确计算整个物体每一点的斜率。虽然任一点的斜率只提供了该点“附近”的局部信息,但我们可以把不同点的信息汇集起来,得到描述物体上任何一点斜率的一般函数。然后,借由“积分法”(integration,亦即微积分里相加与平均,基本上和微分相反的一种计算方法),可以推导出描述整个物体的函数。
如此一来,我们就可以了解整个物体的结构。这其实就是微分几何的核心思想,你可以单从导数所得到的局部信息,获得整个曲面的全盘面貌,揭露每一点上的几何特性或度量。
图2.3 在具有正曲率的曲面如球面,三角形的内角和大于180度,而且看似平行的直线可以相交,例如经线可以交会在南北极点。在曲率为0的平坦表面,亦即欧氏几何的平面上,三角形的内角和等于180度,平行线永远不会相交。在负曲率的曲面如鞍面上,三角形的内角和小于180度,而且平行线间的距离会愈来愈远
高斯与黎曼的几何研究
除了微分几何,高斯对于数学和物理还有许多重大的贡献。对我们的主题而言,高斯影响最深远的贡献或许是他这个惊人的看法:空间中的物体并不是唯一可以弯曲的东西,空间本身也可以是弯曲的。高斯的观点直接挑战了欧氏几何平坦空间的概念,这个概念不仅适用于直觉上平坦的二维平面,同时也适用于三维空间,平坦概念的结果是:即使在很大的尺度时,平行线仍然永远不相交,而且三角形的内角和必定是180度。
这些原理是欧氏几何的基本性质,但在弯曲的空间里却不成立。若以像地球表面的球面空间为例,在赤道上观察时,地球的经线全都垂直于赤道,看来似乎是彼此平行的。但若沿着经线往两端走,它们最后会在南、北极相交。这在平坦的欧氏空间里是不可能发生的,例如在一般的地图上,垂直于同一直线的两直线就必定平行,而且永远不相交。
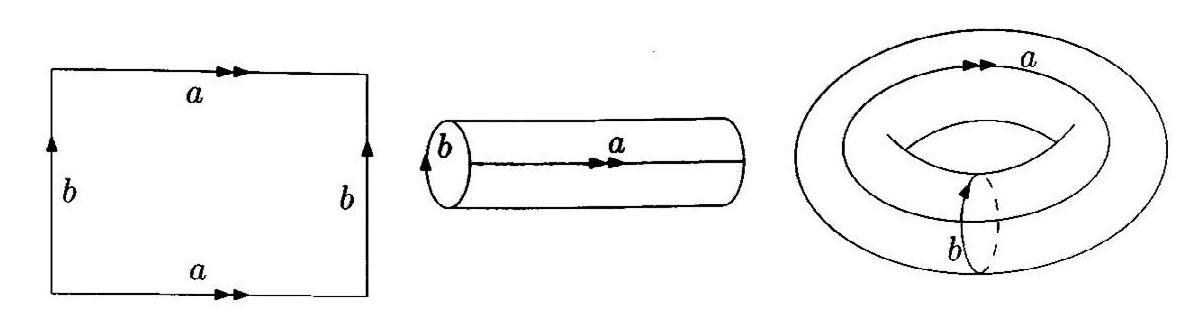
图2.4 一个甜甜圈形的曲面可以是完全“平坦”的(高斯曲率为0),因为原则上,我们可以把一张纸卷成筒状,然后再把纸筒的两端接起来
在非欧空间里,三角形的内角和可以大于180度或是小于180度,视空间的弯曲情形而定。如果是像球面之类的“正”曲率曲面,三角形的内角和会大于180度。反之,如果空间像马鞍的中间部分,曲率是“负”的,则三角形的内角和就会小于180度。反过来说,我们可以借由三角形内角和与180度的偏差程度来测量空间的曲率。
高斯同时也提出了“内禀几何”(intrinsic geometry)的概念,其想法是:物体或曲面有它自己的曲率(所谓的“高斯曲率”),和它在空间中摆放的方式无关。以一张纸为例,你会猜测它的曲率是0,确实如此没错。但如果把这张纸卷成一个圆柱面,根据高斯曲率,像这样的二维曲面有两个方向彼此垂直的“主曲率”(principal curvature),在本例中,一个是圆的曲率,其值为1/r,其中r为圆半径(如果r=1,则此曲率是1);另一个是沿着柱向的曲率,圆柱面的柱向是直线,而直线根本不弯曲,所以它的曲率显然是0。但是二维曲面(包括这个圆柱面)的高斯曲率(曲面的内禀曲率)等于主曲率的乘积,在本例就是1×0=0。由内禀曲率来看,一张纸和由它所卷成的圆柱面是相同的,内禀曲率都是完全平坦。因为一张纸不需要拉扯或扭曲就可以卷成圆柱面,所以圆柱面的内禀曲率是0。换个方式来说,假如有一张纸,不管我们把它摆在桌上或把它卷成筒状,纸上任意两点之间的距离并不会改变。这表示这张纸的几何及其内禀曲率,不会因为它是平坦或卷曲而改变。
与此类似,假如我们能把圆柱面的两端接合起来而做成一个环面,而且在接合时未发生拉扯或变形,这个环面的内禀曲率会和原来的圆柱面相同,也就是0。但是实际上,至少住在三维空间中的我们不可能造出像这样的平坦环面,因为无可避免必会出现弯扭和皱褶。但我们可以在理论上构造这样的物体(称为抽象曲面),而且在数学领域里,抽象曲面的重要性绝不亚于所谓的真实物体。
至于球面,则和圆柱面与环面大不相同。半径为r的球面的高斯曲率是1/r2,在球面上任何点的曲率都是一个正的常数。如此一来,球面上的任何方向看起来都一样,而这在圆柱面和环面上显然不成立。而且不管我们在三维空间中如何摆放这个球面,球的这个性质都不会改变。倘若有只小虫住在球面上,不管球面在三维空间中如何摆放,想必它会无动于衷,它所关心且能经验到的,是它所在的局部、二维区域的几何。
高斯、罗巴切夫斯基(Nikolai Lobachevsky)和波雅伊(János Bolyai)三人极大推进了我们对抽象空间的理解,特别是二维的情况,然而高斯本人也承认对此领域有些困惑。最终,把我们的空间概念完全从欧氏几何架构解放出来的,既不是高斯,也不是他的同辈人。高斯在1817年写给天文学家奥伯斯(Heinrich Wilhelm Matth us Olbers)的一封信里表达了他的迷惑:“我愈来愈相信,我们的几何的必然性是无法证明的,至少无法借由人类理性来证明,或者其证明无益于人类理性。或许在下辈子,我们会对目前无法触及的空间本质有所理解。”[35]
其中有些解答,并不像高斯所写的得等到“下辈子”,而是在下一代经由他的学生黎曼的卓越才智和努力所达成。黎曼多病而早逝,年仅四十岁。但在这段短暂的时间里,他协助推翻了几何学的传统看法,而且在此过程中,也翻转了人们原先认知的宇宙图像。黎曼引入了一种特殊的度规方式,指派给空间或“流形”(manifold)中每一点一组数字(流形是任何维度的空间或曲面,我们将这些词汇当成同义词交替使用,第4章会再细述),这些数字可揭露连接两点间任何路径的距离。而借由此信息,则可决定空间的弯曲程度。
测量空间在一维的情况中最为容易。例如要测量直线之类的一维空间,只要一把尺就够了。如果是二维空间,例如舞池的地板,通常需要两把互相垂直的尺(一个称为x轴,一个称为y轴),你可以以想要测量的两点为斜边画出直角三角形,再用毕氏定理算出距离。三维的情形与此相仿,不过得要三把互相垂直的尺x,y和z。
但如果在弯曲的非欧空间,事情就变得十分复杂有趣了。相互垂直又有适当刻度的尺在此不再适用,我们得依赖黎曼几何的想法来计算距离。计算弯曲流形上一条曲线长度的方法听起来会很熟悉:我们把曲线分割成一段段无穷小的“切向量”(tangent vector),再用积分把整条曲线积起来,便可得到曲线的全长。
棘手之处在于弯曲空间中,当我们在流形上逐点移动时,每段切向量的测量方式也会随之改变。为了处理这种情形,黎曼引入了度规张量,借此来计算每一点上切向量的长度。在二维的情况,度规张量是一个2×2矩阵,而在n维时,度规张量是一个n×n矩阵。值得一提的是,尽管这种测量的新方法是黎曼的伟大创见,它仍然极为仰赖毕氏定理,只是把它推广到非欧几何的情形而已。
具有“黎曼度规”(Riemannian metric)的空间称为“黎曼流形”(Riemannian manifold)。有了黎曼度规,我们就可以测量任意维度的流形上任何曲线的长度。但我们能做的并不仅限于测量曲线长度,我们也可以测量该空间里某一曲面的面积,在此所指的“曲面”并不仅限于一般所指的二维曲面,“面积”也不仅止于一般的二维面积。
借由黎曼度规的发明,原先只能模糊界定的空间,就可被赋予明确描述的几何;曲率不再只是个笼统的概念,而是可以给空间中的每一点都标上精确的数字。而且,黎曼证明了这种想法可以应用到所有维度的空间。
在黎曼之前,弯曲的物体仅能从“外部”来研究,就像从远处来测量山脉,或是从太空船来观察地球表面那样。一旦接近,一切看起来似乎都是平坦的。黎曼演示了,即使别无他物以资比较,我们仍有办法察觉我们是否活在弯曲的空间之中。[36]这带给物理学家和天文学家一个重大问题:如果黎曼是对的,而且我们就只有一个空间,而无法跳脱到一个更上层的结构来观察,这表示我们必须重新调整心目中万事万物的图像:它意味着在最大尺度上,宇宙未必得遵守欧氏几何。空间可以四处游荡,空间可以自由弯曲,空间随便想怎样都可以。正因为如此,天文学家和宇宙学家如今正进行精密的测量,以期得知我们的宇宙是否是弯曲的。多亏了黎曼,我们不必跑到宇宙之外来做这些测量,这是无论如何都难以办到的!现在,我们可以待在原地来找答案,宇宙学家和喜欢窝在沙发上的懒骨头必定都会放心不少。
爱因斯坦的广义相对论
总而言之,当爱因斯坦开始发展他的引力理论时,这些就是当时流行的新几何理念。20世纪之初,爱因斯坦花了近十年的时间,尝试把他的狭义相对论和牛顿的引力论结合起来。他猜测解答的关键可能在几何里,于是向他的朋友,几何学家格罗斯曼(Marcel Grossman)寻求协助。格罗斯曼是爱因斯坦的大学同学,当年爱因斯坦没兴趣的毕业必修课程,还得靠他来帮忙应付。格罗斯曼把当时物理学家还很陌生的黎曼几何介绍给他,不过他警告爱因斯坦,黎曼几何是“一团混乱,物理学家最好别碰”。[37]然而,要解开爱因斯坦缠斗数年的谜团,黎曼几何正好是关键。我们在第1章已提到,当时爱因斯坦正在对付弯曲的四维时空(也就是我们的宇宙)。对他而言真是幸运,因为黎曼正是用这种方式定义空间的,因而提供给他一个现成的理论架构。布莱恩·格林恩(Brian Greene)认为,“爱因斯坦的天才之处在于他一眼就看出,这整套数学正是为他的引力理论新看法量身定做的。他果敢地宣告,黎曼几何的数学与引力物理学是完美契合的”。[38]
爱因斯坦不仅看出黎曼几何可用于描述时空,也看出时空的几何会影响时空的物理学。既然狭义相对论已通过时空观念来统一空间与时间,爱因斯坦接下来的广义相对论便是要进一步将空间与时间,以及物质与引力统一起来。这是概念上的大突破。此前的牛顿物理学把空间视为一种被动的背景,而不是过程中的主动参与者。再想到当时根本没有任何实验结果需要新理论加以解释,爱因斯坦这项突破就显得更为惊人。这想法其实完全是从一个人的脑袋里蹦出来的(当然并不是说,任何一个人的脑袋都能凭空蹦出这种想法)。
物理学家杨振宁将爱因斯坦的广义相对论称为“纯粹创造”之举,“在人类历史中是独一无二的。……爱因斯坦并不是抓住眼前的机会,而是自己创造了机会,然后又独自一人通过深刻的洞识、宏伟的设计实现了这个机会”。[39]
这项卓越的成就或许连爱因斯坦都会感到吃惊。在此之前,他并未看出物理学的基础竟会和数学如此紧密交织在一起。然而,他在多年之后归结道:“创造的原理存在于数学之中。因此在某种意义上,我认为正如古人所梦想的,纯粹的思想便足以理解实在。”[40]爱因斯坦是纯粹经由思考,只通过数学而未借助外在世界的提示,即得到了他的引力论。
具备了黎曼度规张量的知识之后,爱因斯坦开始构想时空的形状及其他性质,亦即时空的几何。他将几何学与物理学融洽在一起,结果淬炼出著名的爱因斯坦场方程式,这组方程式表明了在最大尺度上塑造宇宙形状的引力,可以视为是时空弯曲所造成的某种假象。黎曼几何的度规张量不仅描述时空的曲率,同时也描述了爱因斯坦新理论的引力场。因此,像太阳这样的巨大质量天体所造成时空结构的弯曲,就像大块头的人站在蹦床上,会造成蹦床变形。如果把一粒弹珠弹进蹦床里,它会绕着人旋转,最终掉进他所造成的凹陷里;同理,弯曲时空的几何导致地球绕着太阳旋转。换言之,引力即是几何。物理学家惠勒(John Wheeler)曾如此解释爱因斯坦的引力图像:“质量告诉空间如何弯曲,借以紧抓住空间;空间告诉质量如何移动,借以紧抓住质量。”[41]
再举一个可以阐明这一点的例子:假设有两个人位于赤道上的不同点,以相同速率沿着经线向北极前进。随着时间推移,他们会彼此愈来愈靠近。他们或许会以为是某种看不见的力把两人拉近;但换个方式来看,这其实只是地球形状所造成的结果,根本没有什么力在作用。这个例子可以让我们对引力就是几何的思路有个基本概念。
相对论与我
当我在研究所的第一个学期初次接触广义相对论时,这个理论带给我巨大冲击。我们当然都知道,引力塑造了宇宙,引力是掌握大局的总建筑师。但在较小的尺度,在大多数物理学仪器的狭小范围里,引力比起其他作用力(电磁力、强力、弱力)是非常微弱的。但若提到万物的宏伟架构,大概可说全是由引力完成的,它创造了宇宙的结构,小至个别的星体和星系,大至规模可达十亿光年的巨型超星系团。如果爱因斯坦是对的,而一切都可以归结到几何,那么我们就得承认几何的力量。
当时我坐在课堂上,思考其寓意,此时我的脑海里浮现种种想法。我在大学时就对曲率很有兴趣,照爱因斯坦的洞见来看,这或许是理解宇宙的关键,而且沿着这条路走下去,有朝一日或许我也能做出自己的贡献。微分几何提供了工具来描述物质如何在弯曲的时空中移动,但却未解释时空为何会弯曲。爱因斯坦则利用同样这些工具来解释曲率从何而来。空间在引力影响下的形状,以及空间在曲率影响下的形状,这两个看似完全不同的问题,结果却是同一件事!
再往前走一步,我所思考的问题是这样的:如果来自于质量的引力告诉空间如何弯曲,那么完全无质量的空间,也就是称为真空的空间,会是如何?那时会由何者决定一切?换个说法,爱因斯坦场方程式在真空的情形下,是不是只有一个最没意思的解;也就是说,除了一个没有物质、没有引力、没有相互作用,什么都没有的“平庸”时空之外,是否还有别的可能?我揣想,是否有一个虽然没有物质,但曲率和引力不为零的“不平庸”时空?
我当时还没有能力回答这些问题,而且也不知道有位数学家卡拉比(Eugenio Calabi)早在十五年前即已提出这个问题的某一特例,不过他是以纯数学观点来看待这个问题,不曾考虑引力和爱因斯坦。当时我能做的只是忘形惊叹,纳闷答案究竟如何。
我的学习历程
从许多方面来看,我会问这样的问题非属寻常。特别是考虑到我的成长背景,或许我的出路应该是去养鸡饲鸭,而不是研究几何、广义相对论和弦论。
我在1949年出生于中国内地,但是未及一岁全家即迁居香港地区。我的父亲是位收入不丰的大学教授,还要负担妻子和八个子女的生计。虽然他在三所大学教书,但薪水微薄,实在难以求得温饱。我们家生活贫困,没有水电供应,得到附近的河边洗澡。不过,物质上的匮乏,却在其他方面得到补偿。父亲是位哲学家,他启发我用更抽象的眼光来观照世界。我还记得小时候,从旁听到他和学生及同事的对话,即使不能体会话中含义,也仍能感到其中的激动之情。
父亲总是鼓励我学数学,但我起步并不顺遂。我五岁时,参加一所明星公立学校的入学考试,但是数学没过关。因为我把75写成57,96写成69——我现在会安慰自己,这种错误在中文里会比英文容易犯。结果我只能去读一所较差的乡下学校,跟许多对念书没兴趣的野孩子当同学。为了生存,我得跟他们一样野,以至于小学时有段时间我逃学在外,当一群野孩子的头头,成天到街上惹是生非。
个人悲剧改变了这一切。我十四岁时,父亲意外过世,留下了不仅悲伤而且无助的一家人,背负着大笔债务,却没有任何收入来源。我需要挣钱来养活家人,舅舅建议我休学,改去养鸭。但我却另有想法:当其他学生的数学家教。考虑当时我们家的经济状况,我知道我只有一次的尝试机会,于是我孤注一掷,把全部的赌注都押在数学上。如果不成功,我将无路可退(大概除了养鸭之外),前途全部没了,不会再有第二次机会。我发现,人在绝境时会更勤奋,虽然我或许有种种缺点,但绝不懒惰。

图2.5 几何学家陈省身(照片提供:George M.Bergman)
我的高中成绩不算最顶尖,但我在大学时努力弥补。我在香港中文大学第一年的成绩还不错,但还算不上优异;不过大二时,柏克莱的年轻几何学家萨列弗(Stephen Salaff)来我们学校任教,我的学习开始大有起色。通过萨列弗的启发,我才初次品尝数学的精髓。我们一起教一门常微分方程的课,后来还就此门课合写了一本教科书。萨列弗把我引介给一位柏克莱的杰出数学家萨拉森(Donald Sarason),而萨拉森安排我在大三之后,直接到柏克莱去念研究所。克服跳级入学的重重官僚阻碍是一项艰苦挑战,相较之下,我在此之前所学的数学都要简单得多,幸好得到当时也在柏克莱的著名几何学家陈省身的大力协助,我终于能成行了。
当我在二十岁来到美国加州时,呈现在我眼前的是所有的数学领域,我根本不知道该朝哪个方向发展。一开始我倾向算子代数,因为它是代数中较抽象的一个课题,而我隐约觉得愈抽象的理论愈好。
当时,柏克莱在许多数学领域都很强,但它更是世界级的几何研究中心,甚至可说是全世界最好的:任教的许多著名几何学家,如陈省身,在潜移默化之中影响了我。再加上我逐渐认识到几何是充满了各种可能性的一个丰富领域,于是我慢慢改变初衷,转投几何。
尽管如此,我仍尽量接触各个领域,选修了六门研究所课程,而且还旁听许多课,包括几何、拓扑、微分方程、李群、组合学、数论和概率论。这使得我每天从早上八点上课到下午五点都待在课堂,几乎没有时间吃午餐。如果没课,我就待在数学图书馆,抓住机会什么书都读,那里成了我的第二个家。因为以前买不起书,我就像俗话所说的“进了糖果店的小孩”,看到什么都想要,从书架的这一头读到那一头。既然没有更好的事可做,我常待到关门时刻,往往是馆里的最后一人。孔子曾说过:“吾尝终日不食,终夜不寝,以思,无益,不如学也。”虽然我当时或许没想到这句话,但这却是我奉行的哲学。
为什么在数学的众多分支里,我独独偏爱几何,不论醒着或在梦里,脑海中都是几何呢?主要是因为我觉得几何最接近自然,因此最可能回答我所关切的问题。除此之外,我发现要掌握艰深的概念时,有图辅助对我帮助很大,但是代数和数论一旦进入较深奥的范围时,图示却很稀有。再者,柏克莱有一个绝佳的几何团队,有陈省身和莫瑞(Charles Morrey)等教授,年轻的教师群如劳森(Blaine Lawson),还有研究所的同学如日后的菲尔兹奖得主瑟斯顿(William Thurston),这些都使我乐于成为其中的一员,也希望能有所贡献。
除此之外,不止在美国校园,且遍布全世界(甚至跨越整个数学史,正如我们在本章所看到的),还有一个更宏大的数学社群的努力开拓,才辟建出这一片我有幸涉足其中的沃土。这就像牛顿所说的“站在巨人的肩膀上”,当然,牛顿自己又是巨人中最魁伟的一位。
大约就在我开始思索爱因斯坦的广义相对论和真空中的空间曲率之时,我的导师陈省身从东岸回来,兴奋地说道,他刚从普林斯顿的大数学家威尔(André Weil)那里听说,一个多世纪悬而未决的“黎曼假说”或许很快就能解决了。黎曼假说和质数的分布有密切关系。质数的分布并没有什么明显的规律,但黎曼猜想质数出现的频率和一个称为“黎曼ξ函数”的复变函数有关。更详细地说,黎曼认为质数出现的频率与ξ函数的根值分布有密切关系。经过数值计算确认,黎曼假说知道十亿个根值的位置都是正确的,但是迄今仍未有完整的证明。
虽然这是整个数学界最显赫的问题之一,谁能解决它,不但可以确保工作无虞,而且可以在数学史上留名;但我对陈省身的提议不太热衷。黎曼假说就是无法激起我的热情,而如果你下决心要研究一个令众多英才铩羽而归,而且最少得钻研经年的重要问题,你得要有热情才行。热忱不足无疑会影响成功的机会,也就是说,我可能会研究黎曼假说多年,却毫无成果。再加上我实在非常喜欢图像的表示,喜欢能以某种方式观看的数学结构,这就是我偏爱几何的原因。更何况在几何的某些领域里,我已经知道我可以做出一些成绩,尽管远不如黎曼假说那么辉煌。
这就好像钓鱼。如果对鱼的大小没那么挑剔,你通常总能带点东西回家。但如果你只想钓到没人捕获过的大鱼,像是神话传说中的巨物,那你几乎注定空手而归。二十五年过去了,黎曼假说依然是未解的问题。就像我们常说的,数学里没有已经证明了90%这回事。
我之所以谢绝陈省身的提议,部分原因即在此,但是我还有更重要的理由。正如前文所云,我已对广义相对论感到着迷,想要了解从引力、曲率和几何的互动中所产生的宇宙特征。我还不知道这个研究方向会把我带到哪里,但我有预感:驾驭几何的力量追求真理,将会是一趟万分精彩的历程。
对于一个出身清寒的人,我没机会到过多少地方。但我从小就对几何怀抱热情,希望能为如中国一般的大地描绘地图,旅历诸多不知有岸的汪洋。后来,虽然到过的地方多了,但几何对我的意义始终如一,只是现在我想到达的是整片大地与汪洋,以及浩瀚的宇宙。而当年随身带着的草编小包袱,现在已经换成了公事包,里面装着直尺、圆规和量角器。